完美滤波器

如下图所示，第j级为输入图像，其中第j-1级为第j级的尺寸减半的存在，直至为 1\times 1 的大小，这样的模式被称为图像金字塔

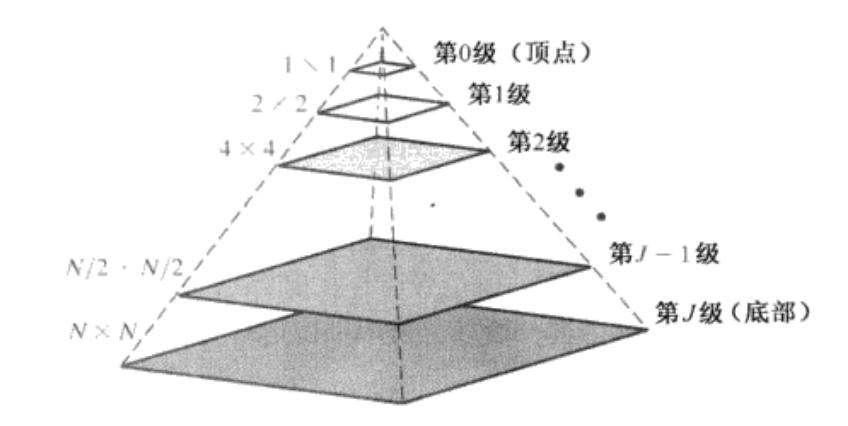
设原图像像素点个数为 N^2，则图像金字塔的总像素个数为

对于图像金字塔建模，设第j级为图像降低分辨率后的近似图像，这可以视为由第j+1 级图像经过滤波操作和下采样实现后的存在，则第j+1级可以视为第j级经过上采样和插值操作后的存在，即如下图所示：

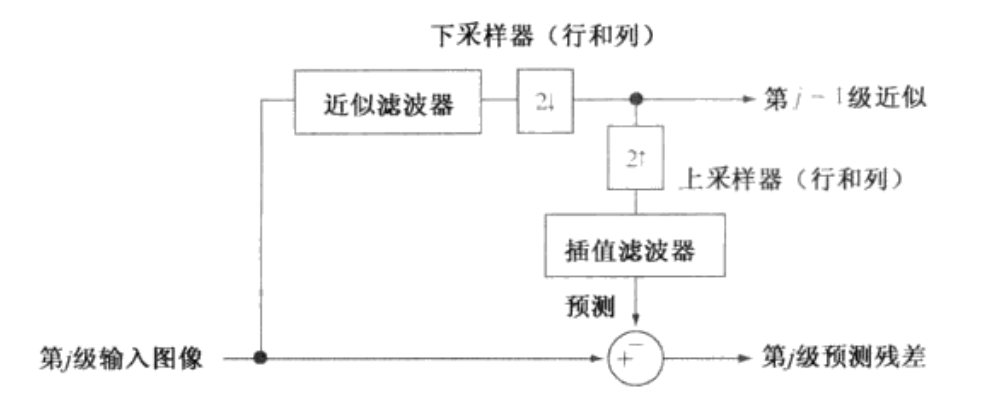
其中对图像进行上采样操作，索引所对应的值为：

图像进行下采样操作，索引所对应的值为：

上采样可看成是在序列中的每一个样本后插人 0; 下采样可看成是每隔一个样本丢弃一个样本。

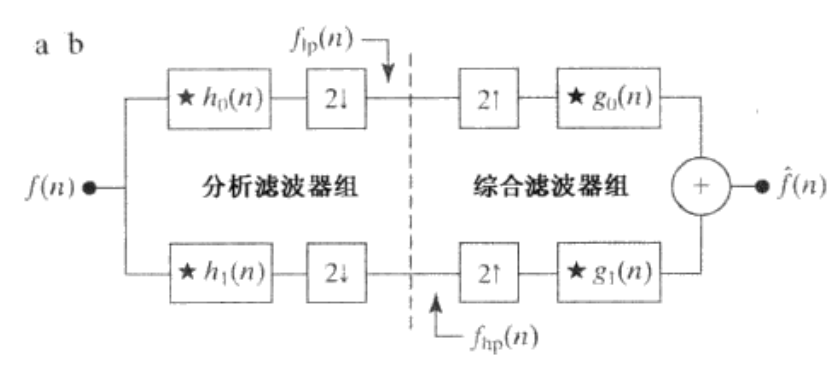
设存在输入信号 f(n)，其中 h_0(n)与 h_1(n) 分别为低通与高通滤波器，并输入信号一分为二，如下图所示

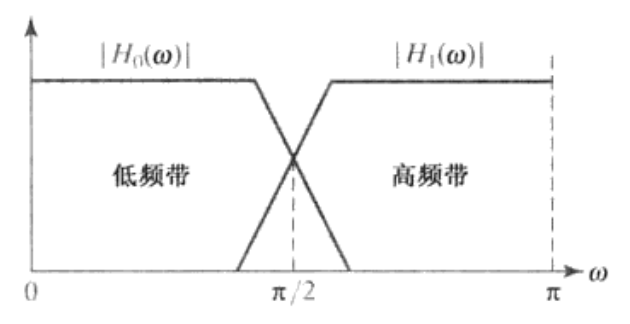
并经过下采样得到 f_{lp}(n)与 f_{hp}(n)。然后经过上采样，与滤波 g_0(n)和 g_1(n)并将信号 f_{lp}(n)与 f_{hp}(n)合并得到信号 \hat f(n)，若 \hat f(n)与 f(n)相等，可以称为采用了完美滤波。

存在一个Z变换:

其中离散傅里叶变换是Z变换的一个特殊形式，即 z=e^{jw}

若对z变换采用下采样，则可以得到:

证明补充：

对信号 x(n)进行下采样处理，则可以得到 x_{\mathrm{dowm}}(n)=x(2n)

设信号 y(n)=x_{\mathrm{dowm}}(n)，则存在Z变换：

\begin{aligned} Y(z) &=\sum_{-\infty}^\infty y(n)z^{-n}\\ &=\sum_{-\infty}^\infty x_{down}(n)z^{-n}\\ &=\sum_{-\infty}^\infty x(2n)z^{-n}\\ \end{aligned}

令t=2n ，则存在

\begin{aligned} Y(z) &=\sum_{-\infty}^\infty x(2n)z^{-n}\\ &=\sum_{-\infty}^\infty x(t)z^{-\frac{t}{2}} \end{aligned}

因为t=2n为偶数，但是此时t为所有整数，所以应该保证t为奇数是为0

所以构造

\begin{aligned} Y(z) &=\frac{1}{2}\left[\sum_{-\infty}^\infty x(t)z^{-\frac{t}{2}} +\sum_{-\infty}^\infty (-1)^{(t)} x(t)z^{-\frac{t}{2}}\right]\\ &=\frac{1}{2}\left[\sum_{-\infty}^\infty x(t)(z^{-\frac{1}{2}})^t +\sum_{-\infty}^\infty (-1)^{(t)} x(t)(z^{-\frac{1}{2}})^t\right]\\ &=\frac{1}{2}\left[\sum_{-\infty}^\infty x(t)(z^{-\frac{1}{2}})^t +\sum_{-\infty}^\infty x(t)((-z)^{-\frac{1}{2}})^t\right]\\ &=\frac{1}{2}[X(z^{\frac{1}{2}})+X(-z^{-\frac{1}{2}})] \end{aligned}

若对z变换采用上采样，则可以得到:

先对信号进行下采样然后进行上采样可得：

根据z变换的逆变换可得：

在根据完美滤波原理：

为了实现完美滤波则，应存在

即：

利用克拉默法则可得

其中 \det(H_m(z))=\alpha z^{-(2k+1)}，忽略时延，并令 \alpha=2，可得

即当 g_0(n)=(-1)^nh_1(n),g_1(n)=(-1)^{n+1}h_0(n)或 g_{0}(n)=\left(-1\right)^{n+1}h_{1}(n),g_{1}(n)=\left(-1\right)^{n}h_{0}(n)时，成立

其中 g_0与 g_1分别由 h_1和 h_0调制得到

因为 H_0(z)G_0(z)+H_1(z)G_1(z)=2

所以存在：

其中 \delta(n)为单位脉冲函数

当n为奇数时将会出现相消得情况，于是可以简化为

可以看成两个向量的内积，同理存在

即 h_{0}(n),h_{1}(n),g_{0}(n)\text{和 }g_{1}(n)满足双正交

即